Компьютерное моделирование позволяет при помощи расчётных методов, таких как, метод конечных элементов, метод конечных разностей, метод конечных объёмов, оценить, как поведёт себя объект – здание, газовая скважина, насыпь дороги, опора трубопровода и др. – в реальных условиях эксплуатации. Моделирование помогает убедиться в эффективности и надежности принятых проектных решений с минимальными временными и материальными затратами.
Для компьютерного моделирования искусственного замораживания грунтов используется специализированное программное обеспечение — Frost 3D, где с помощью численных методов осуществляется решение уравнения теплопроводности с граничными условиями:

![]()
где ![]() — температура;
— температура; ![]() — время;
— время; ![]() — зависимость теплопроводности от температуры;
— зависимость теплопроводности от температуры; ![]() — объемная теплоемкость воды;
— объемная теплоемкость воды; ![]() — скорость фильтрации;
— скорость фильтрации; ![]() — источники и стоки тепла;
— источники и стоки тепла; ![]() — коэффициент теплообмена;
— коэффициент теплообмена; ![]() — температура внешней среды;
— температура внешней среды; ![]() — температура источника теплового излучения;
— температура источника теплового излучения; ![]() — степень черноты поверхности грунта;
— степень черноты поверхности грунта; ![]() — постоянная Стефана – Больцмана;
— постоянная Стефана – Больцмана; ![]() — тепловой поток, например с испарителя охлаждающего устройства.
— тепловой поток, например с испарителя охлаждающего устройства.
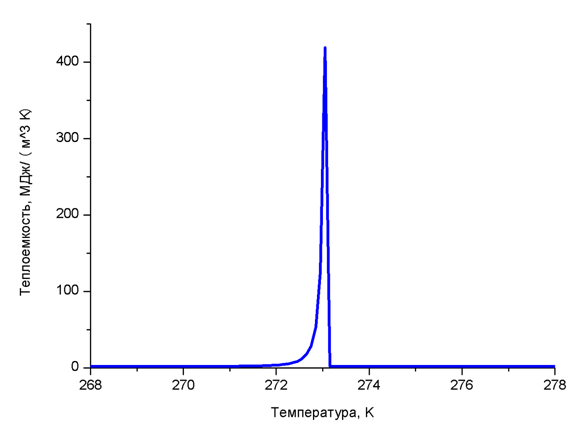
Эффективная теплоемкость и теплопроводность грунта могут задаваться в виде зависимостей от температуры либо вычисляться по соответствующим уравнениям.
|
Зависимость теплоёмкости от температуры
|
Зависимость теплопроводности от температуры |
Наиболее широкое распространение для вычисления эффективной теплоемкости и теплопроводности получили уравнения вида:

![]()
где ![]() — теплопроводность талого и мерзлого грунта соответственно;
— теплопроводность талого и мерзлого грунта соответственно; ![]() — объемное влагосодержание грунта;
— объемное влагосодержание грунта; ![]() — зависимость льдистости от температуры, которая может быть аппроксимирована следующей эмпирической зависимостью:
— зависимость льдистости от температуры, которая может быть аппроксимирована следующей эмпирической зависимостью:

![]() — температура фазового перехода вода-лед;
— температура фазового перехода вода-лед; ![]() — эмпирический коэффициент, который определяет крутизну изменения льдистости от температуры в окрестности фазового перехода.
— эмпирический коэффициент, который определяет крутизну изменения льдистости от температуры в окрестности фазового перехода.
Уравнение теплопроводности с граничными условиями решается для трехмерной области, которая анализируется при проектировании объекта. Данная область, как правило, включает в себя геолого-литологические слои грунта, проектируемые основания и фундаменты, теплоизоляционные слои, устройства для охлаждения грунта и другие элементы.

Область моделирования участка для искусственного замораживания грунта
За верхнюю границу области моделирования, как правило, принимают поверхность земли, а нижнюю границу располагают на достаточно большой глубине, чтобы минимизировать её влияние на тепловые процессы в интересующей проектировщика области.
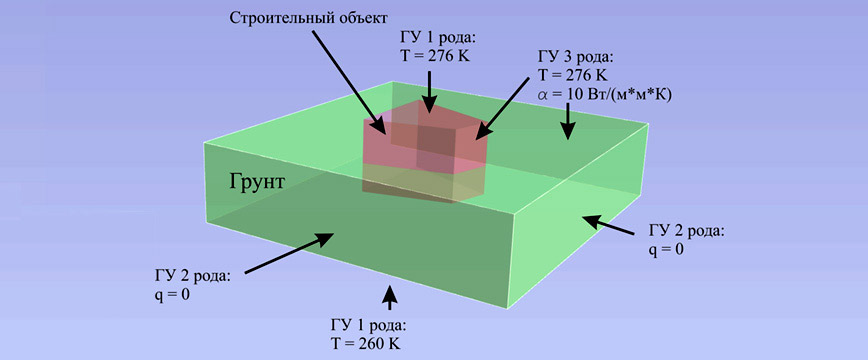
На верхней границе области моделирования задаются условия теплообмена с окружающей средой, которые определяются температурой воздуха и коэффициентом теплообмена. При наличии источников теплового излучения, например, факела сжигания попутного газа, дополнительно задается температура источника излучения и степень черноты поверхности грунта. Учет влияния снегового покрова на теплообмен поверхности грунта осуществляется путем задания изменения во времени толщины снежного покрова и его теплопроводности.
На нижней границе области моделирования задается температура грунта согласно термометрическим данным. На боковой поверхности области моделирования, как правило, задается нулевой тепловой поток. При этом боковые границы области моделирования должны быть расположены достаточно далеко от интересующего проектировщика участка, чтобы они не оказывали влияние на расчет тепловых процессов.
Задание граничных условий на области моделирования при прогнозировании теплового режима грунтов
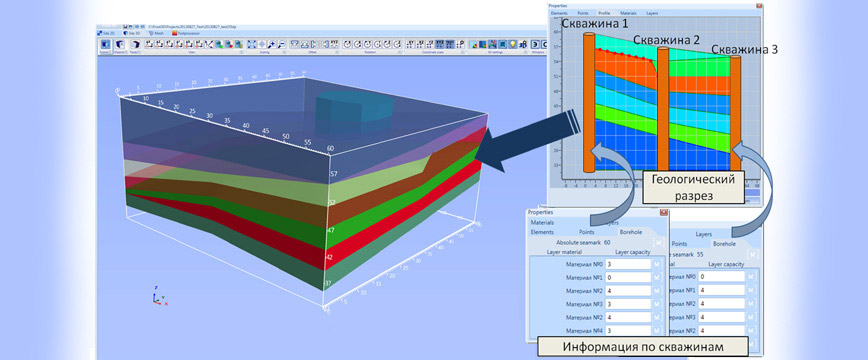
Следует отметить, что область моделирования состоит из неоднородных слоев грунта, с различными теплофизическими свойствами – теплоемкостью, теплопроводностью, плотностью и влагосодержанием. В связи с этим для компьютерного моделирования искусственного замораживания грунтов необходимо построение трехмерной области моделирования, в которой учтено реальное распределение слоев грунта с различными теплофизическими свойствами. Такое распределение слоев грунта строится на основании данных, полученных по инженерно-геологическим скважинам. При сложном строении грунтов для восстановления области моделирования необходимо использовать методы геостатистики.
Восстановление геолого-литологического строения грунтов на основании инженерно-геологических скважин
Поскольку для решения уравнения теплопроводности в трехмерной постановке необходимо использовать численные методы, область моделирования дискретизируется расчетной сеткой. Для моделирования тепловых процессов в грунтах для больших пространственных масштабов оптимально использовать гексаэдрическую расчетную сетку. В результате дискретизации заданные пользователем теплофизические свойства грунтов и граничные условия переносятся на соответствующие элементы и грани элементов расчетной сетки.
Дискретизация области моделирования гексаэдрической сеткой
В результате численного решения уравнения теплопроводности получается трехмерное распределение температур в моделируемой области для различных моментов времени. Полученное тепловое поле используется для анализа тепловых режимов грунтов и изменения их механических свойств. На основании анализа принимается решение по обеспечению несущей способности грунтов.